


Next: Network Control
Up: Network Design and Control
Previous: The One-Transition and Two-Transition
We can use the source model
to investigate the value of
information.
We can consider how prediction is improved when we condition on, first,
only the level and, second, on both level and age.
The reference case is the steady-state mean
|  |
(27) |
where pji is the steady-state probability, i.e.,
| 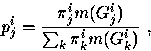 |
(28) |
with 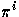 the steady-state vector of the Markov chain Pi
the steady-state vector of the Markov chain Pi
 and m(Gij ) the mean of Gij
for Gj in (8), for all sources i.
With the steady-state mean,
there is no conditioning.
Section 2 gives the formula for conditioning on both level and age.
Now we give the formulas conditioning only
on the level; i.e., we condition on the level, assuming that we are in
steady-state. We omit the i superscript.
Then the age in level j has the stationary-excess cdf
and m(Gij ) the mean of Gij
for Gj in (8), for all sources i.
With the steady-state mean,
there is no conditioning.
Section 2 gives the formula for conditioning on both level and age.
Now we give the formulas conditioning only
on the level; i.e., we condition on the level, assuming that we are in
steady-state. We omit the i superscript.
Then the age in level j has the stationary-excess cdf
| 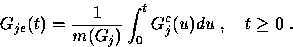 |
(29) |
Let Pjk (t) be the probability of being in level k at time t
conditional on being in level j in steady state at time 0.
Let 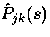 be its Laplace transform.
Let mj (t) be the conditional steady-state
mean given level j at time 0
and let
be its Laplace transform.
Let mj (t) be the conditional steady-state
mean given level j at time 0
and let 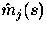 be its Laplace transform:
Clearly
be its Laplace transform:
Clearly
| 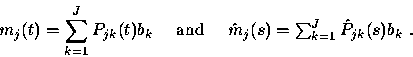 |
(30) |
Hence, it suffices to calculate 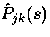 .
.
Theorem 6936
Assume that the level-holding-time cdf depends only on the
originating level, i.e.,
Fjk (t) = Gj (t).
The steady-state transition probabilities conditional on the
level for a single SMP source have the matrix of Laplace transforms
|  |
(31) |
where 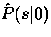 is the matrix in
(14),
is the matrix in
(14), 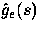 is the
matrix with elements
is the
matrix with elements
| 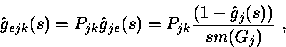 |
(32) |
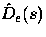 is the diagonal matrix with diagonal elements
is the diagonal matrix with diagonal elements
| 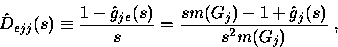 |
(33) |
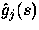 is the level-j holding-time LST and
is the level-j holding-time LST and 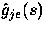 is the LST of
its stationary-excess cdf in (32).
is the LST of
its stationary-excess cdf in (32).
Proof.
Modify the proof of Theorem 2.1, inserting Pjl Gje(t)
for Hjl (t|x) and
Gjec (t) for Gjc (t|x).
Example 4.1.
Consider the on-off source in Example 2.1.
Paralleling (17), it suffices to
calculate only P12(t).
Its Laplace transform is
|  |
(34) |
Example 4.2.
To show the value of knowing the age, consider an on-off source with
holding-time ccdf's
| 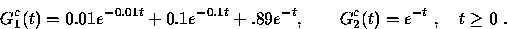 |
(35) |
Let the bandwidths be b1 = 100 and b2 = 0.
Since m(G1 ) = 2.89 and m(G2 ) = 1.00,
the steady-state mean is
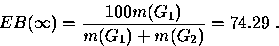
Let the initial level be 1.
Since G1 has an exponential component with mean 100,
we anticipate the time to reach steady state to be
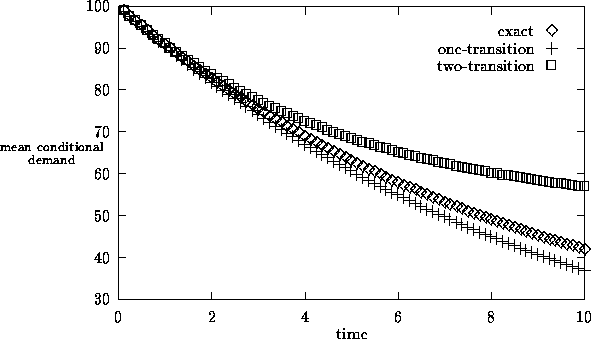
between 100 and 1000.
In Figure 2 we plot the conditional mean m1 (t|x)
for x = 0.5, 5.0 and 50.0,
computed by numerical transform inversion.
Figure 2 shows that the age plays a very important role.
Figure 2:
The conditional mean aggregate demand as a function
of the age of the holding time in level 1 for Example 4.2.
 |



Next: Network Control
Up: Network Design and Control
Previous: The One-Transition and Two-Transition
Nick Duffield
11/24/1997


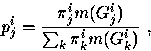
![]() be its Laplace transform.
Let mj (t) be the conditional steady-state
mean given level j at time 0
and let
be its Laplace transform.
Let mj (t) be the conditional steady-state
mean given level j at time 0
and let ![]() be its Laplace transform:
Clearly
be its Laplace transform:
Clearly
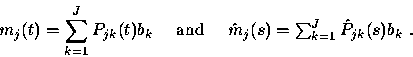
![]()
