Our aim now is to prove that if ![]() can be derived in our
logic from
can be derived in our
logic from ![]() together with (some yet-to-be-defined
logic translation
of)
together with (some yet-to-be-defined
logic translation
of) ![]() , then
, then ![]() holds. From that we can conclude a rectified version, so that we know
that participants in protocols draw correct conclusions.
holds. From that we can conclude a rectified version, so that we know
that participants in protocols draw correct conclusions.
As we have seen, the sending of a message is modelled by adding the
message to the sender's ![]() set of messages once-said, and to the
receiver's
set of messages once-said, and to the
receiver's ![]() set of messages seen, and then to apply the closure as
mentioned in section 4. We now define the logical
equivalent of this:
set of messages seen, and then to apply the closure as
mentioned in section 4. We now define the logical
equivalent of this:
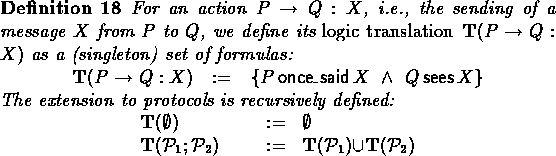
Proof
Let ![]() be
be ![]() .
.
![\begin{calc}
\xpr{\models
\spec{\emptyset}{\send{P}{Q}{X}}{\predprot{\send{P}{Q}...
...Q\becomes\Sees_Q\union\{X\}])
\models P \oncesaid X \land Q \sees X}\end{calc}](img171.gif)
Now let s be any state,
and put ![]() .We have
.We have

![]()
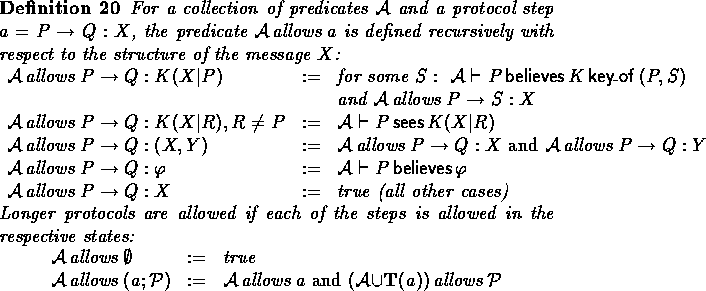
Proof
We prove ![]() from
from ![]() with induction on X .
with induction on X .


![]()

This is extended to finite sets of formulas:
![]() is positive whenever the formula
is positive whenever the formula ![]() is.
is.
This follows immediately from the following lemma:
The proof of this lemma can be found in the appendix.
![]()
![]()
The following lemma follows immediately from the definition of safe.
![]()
We now formulate Lemma 23 for the weaker requirement of
![]() being safe, rather than positive.
being safe, rather than positive.
The proof of this lemma can be found in the appendix.
![]()

From Theorem 9 our main theorem now follows: a proof of a specification in the logic indeed ensures the right conclusions of the principals during the protocol.
![]()
