The intent hereafter is to present the verification algorithm. First of all, we would like to present an algebraic formalization of the message domain. The latter is defined in terms of a many sorted ordered algebra.
Definition 4.1 (Signature)
An order-sorted signature ![]() is a pair
is a pair
![]() where
where ![]() is a partially
ordered set of sorts (type names) and
is a partially
ordered set of sorts (type names) and ![]() is a set of function
symbols. Each function symbol f is associated with an arity i.e. a
finite word of the form
is a set of function
symbols. Each function symbol f is associated with an arity i.e. a
finite word of the form ![]() where
where ![]() ranges over the domain
ranges over the domain ![]() . The function f is said
to be of arity n . The term
. The function f is said
to be of arity n . The term ![]() is called the
domain of the function f while
is called the
domain of the function f while ![]() is called the codomain of
f . Functions with arity are called constants.
is called the codomain of
f . Functions with arity are called constants.
In order to lighten the notation, we will use, in the sequel, ![]() to denote a signature
to denote a signature ![]() .
.
Definition 4.2 (![]() -Algebra)
-Algebra)
Let ![]() be an order-sorted signature. An
order-sorted
be an order-sorted signature. An
order-sorted ![]() -algebra is a pair (
-algebra is a pair (![]() ,
,![]() ) where
) where
![]() is an
is an ![]() -indexed family of sets, say
-indexed family of sets, say ![]() , and
, and ![]() is a
is a
![]() -indexed set of functions
-indexed set of functions ![]() ,such that for all sorts s and s' ,
,such that for all sorts s and s' , ![]() implies
implies ![]() . Moreover, if
. Moreover, if ![]() then
then ![]() .
.
Definition 4.3 (Free Algebra)
Let ![]() be
an order-sorted signature and X be an
be
an order-sorted signature and X be an ![]() -indexed set of
variable identifiers or merely variables i.e.
-indexed set of
variable identifiers or merely variables i.e. ![]() such that
such that ![]() . The free
. The free ![]() -algebra over X is the pair
-algebra over X is the pair
![]() where:
where:
The next definition introduces formally the algebra of messages used within this work. First of all, we consider the following sorts: Msg , Key , Nonce , Agt , Nat and Server that classify respectively messages, keys, nonces, agents, naturals and the server. We consider these function symbols: e , c , key , nonce , agt that correspond respectively to encryption, catenation, key generation, nonce generation and agent generation. In addition, we assume the existence of a constant s denoting the server. Let, and succ be the usual natural constructors. The arities of these functions are given below:
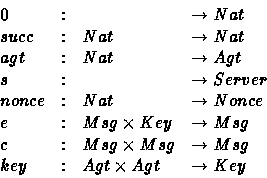
Definition 4.4 (Message Algebra)
Let ![]() be the sort set
be the sort set ![]() and
and ![]() be the function symbol set
be the function symbol set
![]() . Let
. Let ![]() be an
be an
![]() -indexed family of message variables. We endow
-indexed family of message variables. We endow
![]() with a partial order
with a partial order ![]() which stipulates
that
which stipulates
that ![]() ,
, ![]() ,
, ![]() ,
, ![]() and closed under reflexivity. We define the
algebra of messages
and closed under reflexivity. We define the
algebra of messages ![]() as the free
as the free
![]() -algebra over
-algebra over ![]() . The free terms of the latter
algebra are called messages.
. The free terms of the latter
algebra are called messages.
In what follows, we present formal definitions of roles and protocols.
Definition 4.5 (Protocol)
A protocol is a sequence of communication steps. Each step is
a triple of the form ![]() where A and B are
principal identifiers, and m is a message. A triple
where A and B are
principal identifiers, and m is a message. A triple
![]() has to be read as: A sends the message m to
B .
has to be read as: A sends the message m to
B .
Definition 4.6 (Role)
A role is a sequence of communication steps. Each step is a
triple of the form ![]() where P is a principal
identifier, m is a message and
where P is a principal
identifier, m is a message and ![]() . A triple
. A triple
![]() has to be read as: wait for receiving the
message m from the principal P . A triple
has to be read as: wait for receiving the
message m from the principal P . A triple ![]() has to be read as: send the message m to the principal P .
has to be read as: send the message m to the principal P .
From the protocol definition, it is straightforward how we can extract roles. A role P , for instance, is extracted from the protocol by looking at all the steps (in the same order) in which the character P is used to point out the sender or the receiver.
Table 5:
The Verification Algorithm: Part I

The verification algorithm is reported in Tables 5 and 6. We assume that each principal comes with the specification of two sets KI(R) and Fresh(R) . The set KI(R) corresponds to the initial knowledge of the principal R . Generally, the set KI(R) includes the identity of the role R , the server identity (if it exists), the identities of the other roles and all the keys that he shares with other principals. The set Fresh(R) includes all those fresh messages generated by the role R .
In Tables 5 and 6, we present the main functions invoked by the verification algorithm. The functions reported in Table 5 operate on messages while the functions reported in Table 6 operate on roles.
First of all, let us explain the functions operating on
messages. The Function Glan : takes as parameter a role, say
R , and yields a message set, say M . The latter embodies
all those messages received by R during all the protocol
steps. Given a message set M , the Function Reduce computes
a reduced message set by recursively decomposing and
decrypting (with known keys) those messages in M . For
instance, ![]() yields
yields
![]() . The function Reduce is
used essentially to perform role abstraction, therefore to
generate rules of the inference system. Given a message set
M , the function Flat computes a flattened message set by
recursively decomposing and decrypting non-elementary messages
in M . For instance,
. The function Reduce is
used essentially to perform role abstraction, therefore to
generate rules of the inference system. Given a message set
M , the function Flat computes a flattened message set by
recursively decomposing and decrypting non-elementary messages
in M . For instance, ![]() yields
yields
![]() . The function Flat is used to
generate the side conditions of the inference rules. After the
computation of the premise and the conclusion parts, the side
condition is generated. For example, if we want to know the
side condition of the rule
. The function Flat is used to
generate the side conditions of the inference rules. After the
computation of the premise and the conclusion parts, the side
condition is generated. For example, if we want to know the
side condition of the rule ![]() and the set of fresh messages is
and the set of fresh messages is ![]() . Then, we compute
. Then, we compute ![]() and we
put as side condition
and we
put as side condition ![]() . Hence, the rule the
complete rule is
. Hence, the rule the
complete rule is ![]() .
.
The Function Bind takes as parameter a message set M and
yields a set of bindings. A binding is a pair (m,X) where
the first component is a message and the second component is a
message variable. The Bind function aims to bind all the
messages in M to newly allocated message
variables. Actually, in the verification algorithm, the Bind
function will be invoked with the set of unknown messages to
some role and hence replacing (or binding) these messages by
(or to) variables. The Function Gen takes as parameter a
message m together with a binding set B and yields the
argument message m in which we replace all the messages
occurring in B by their corresponding variables. Indeed, the
function Gen rewrites a message according to a binding. For
instance, given the binding ![]() , the message
m=e(e(m,k),k') will be rewritten into m'=e(X,k') . The
message m' denotes the interpretation of the message m by
a role for which the key k is unknown.
, the message
m=e(e(m,k),k') will be rewritten into m'=e(X,k') . The
message m' denotes the interpretation of the message m by
a role for which the key k is unknown.
Now, we would like to explain the functions that generate the
rules and the constraint set. Recall that, the constraint set
tells us which messages the intruder has to find in order to
attack the protocol. The Function GenRole takes as
parameters a role R , an initial knowledge (message set) KI
and a set of fresh messages (those messages created by the
protocol specifically for a particular session) Fresh . The
computation is done step by step along the protocol steps. The
function GenRole gives as outcome the generalized version of
the role R . The computation of such a generalized role
involves the computation of the corresponding binding and
rewriting the role accordingly. Indeed, at first we collect
M , the set of messages received by R before the current
analyzed step. This is captured in the function GenRoleStep
by Role1 which is initially ![]() . Hence
M=Glan(Role1) . To obtain the reduced set associated with
M , say RM , and taking into account that we have an initial
knowledge (message set) KI and a set of fresh messages
Fresh , we compute
. Hence
M=Glan(Role1) . To obtain the reduced set associated with
M , say RM , and taking into account that we have an initial
knowledge (message set) KI and a set of fresh messages
Fresh , we compute ![]() . At this
point, it is straightforward to see that those messages in
. At this
point, it is straightforward to see that those messages in
![]() ) are unknown to the role
R . Those messages are then used to compute the binding B
according to which the transmitted message in the current step
will be generalized. The inference rules are computed so as to
associate one rule per protocol step. In other words, we
associate one inference rule per output communication made by
a particular role. The function RoleRules(GRole,KI,Fresh)
takes as input the generalized role GRole , the initial
knowledge KI and the fresh informations Fresh associated
with one role. If in the current step the role sends a
message, then the rule premises set includes all the
generalized messages received by this role before this current
step and the conclusion is the message sent at that step. The
rule side condition is pointed out by looking if the premises
set contains a fresh information vis-à-vis this
role. However, if at the current step the role receives a
message, we have only to update the premises set by adding
this message. To generate the complete inference system, we
have to apply the function RoleRules(GRole,KI,Fresh) to all
generalized roles in the protocol. For instance, we remark
that we associate to each step in the protocol an inference
rule, since whenever one role receives a message there is
necessary another which has sent it. Furthermore, since there
is one message sent per protocol step, we generate one rule
for each protocol step.
) are unknown to the role
R . Those messages are then used to compute the binding B
according to which the transmitted message in the current step
will be generalized. The inference rules are computed so as to
associate one rule per protocol step. In other words, we
associate one inference rule per output communication made by
a particular role. The function RoleRules(GRole,KI,Fresh)
takes as input the generalized role GRole , the initial
knowledge KI and the fresh informations Fresh associated
with one role. If in the current step the role sends a
message, then the rule premises set includes all the
generalized messages received by this role before this current
step and the conclusion is the message sent at that step. The
rule side condition is pointed out by looking if the premises
set contains a fresh information vis-à-vis this
role. However, if at the current step the role receives a
message, we have only to update the premises set by adding
this message. To generate the complete inference system, we
have to apply the function RoleRules(GRole,KI,Fresh) to all
generalized roles in the protocol. For instance, we remark
that we associate to each step in the protocol an inference
rule, since whenever one role receives a message there is
necessary another which has sent it. Furthermore, since there
is one message sent per protocol step, we generate one rule
for each protocol step.
The Function Collect is devoted to the collection of those
constraints needed to perform a masquerade on a role R . The
function Collect takes as parameter the generalized role R
and the set of messages K , and returns the set of
constraints. Initially, the message set K is set to ![]() . Whenever the role R sends (output
communication) a message, the intruder adds it to his
knowledge K . When the role is waiting for some message, say
m , the algorithm generates a constraint of the form
(K,Rules,m) which should be read as follows: the intruder
has to synthesize the message m thanks to the proof system
Rules (inference rules) and also by using his knowledge K .
. Whenever the role R sends (output
communication) a message, the intruder adds it to his
knowledge K . When the role is waiting for some message, say
m , the algorithm generates a constraint of the form
(K,Rules,m) which should be read as follows: the intruder
has to synthesize the message m thanks to the proof system
Rules (inference rules) and also by using his knowledge K .
Table 6:
The Verification Algorithm: Part II
