Case Study

In this section, we illustrate the application of our algorithm to the corrected version of the Woo and Lam protocol of Table 2. We will see that new flaws have been automatically discovered. First of all, here is the roles as extracted by the algorithms:

$$Role(A) = \mbox{$\langle {!, A, B} \rangle$} \mbox{$\langle... ... \rangle$} \mbox{$\langle {!, \{N_b\}_{k_{as}},B} \rangle$}$$

$$\begin{array} {lcl} Role(B) & = & \mbox{$\langle {?, A, A} ... ...$\langle {?, \{ A, N_b \}_{k_{bs}} , S} \rangle$} \end{array}$$

$$Role(S) = \mbox{$\langle {?, (A, B, \{N_b\}_{k_{as}}) , B} \... ...le$} \mbox{$\langle {!, \{ A, N_b \}_{k_{bs}} , B} \rangle$}$$

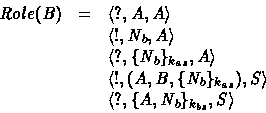
Their associated generalized roles are respectively:

$$Role(A) = \mbox{$\langle {!, A, B} \rangle$} \mbox{$\langle... ...B} \rangle$} \mbox{$\langle {!, \{X\}_{k_{as}},B} \rangle$}$$

$$\begin{array} {lcl} Role(B) & = & \mbox{$\langle {?, A, A} ... ...$\langle {?, \{ A, N_b \}_{k_{bs}} , S} \rangle$} \end{array}$$

$$Role(S) = \mbox{$\langle {?, (A, B, \{X\}_{k_{as}}) , B} \rangle$} \mbox{$\langle {!, \{ A, X \}_{k_{bs}} , B} \rangle$}$$

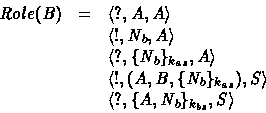
The generalized roles are used by the function RoleRules(GRole,KI,Fresh) to generate the inference system. This step yields the rules shown in Table 7. Since the protocol is a one way authentication, the intruder try only to convince a principal playing a role B that it is a principal A. Let IS be the inference system and KI the intruder initial knowledge,according to the B 's generalized role the constraint set is:

  Table 7:   The Deductive Proof System Associated with the Corrected Version of Woo and Lam Protocol

$$\left \{ \begin{array} {lcl} KI & \models_{IS} & A \\ KI\... ..._b\}& \models_{IS} &\{A, N_b \}_{k_{bs}} \end{array} \right.$$

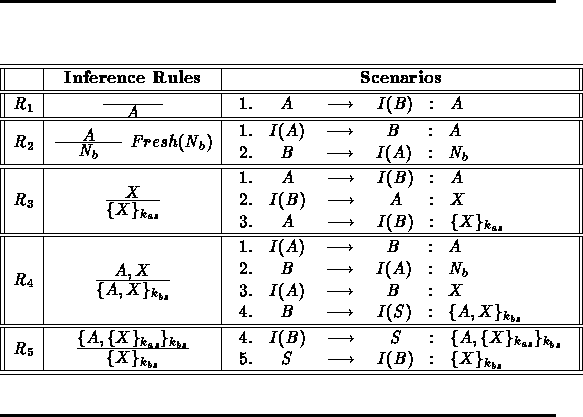
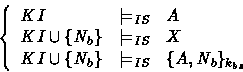
The resolution step yields the two following attacks:

• Attack 1: $$\begin{array} {lccccl} 1.1& I(A)~&\longrightarrow&~B&:&A\\ ... ...5& I(S)~&\longrightarrow&~B&:&\{A,N_b\}_{k_{bs}}\\ \end{array}$$

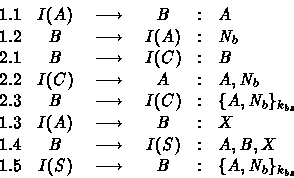
  In this attack, the intruder uses two sessions in order to convince a principal playing B 's role that he is the principal A. Here, the intruder meets no difficulties to supply B with the required messages except the last one, $\{A,N_b\}_{k_{bs}}$. For that reason, the intruder waits for B to begin a session with some principal, say C . For instance, I intercepts the B 's message and replies by $A,N_a$ as a C nonce. Hence, it obtains the message $\{A,N_b\}_{k_{bs}}$ at step 2.3 by which it completes the masquerade in session one.

• Attack 2:

  $$\begin{array} {lccccl} 1.1& I(A)~&\longrightarrow&~B&:&A\\ ... ...5& I(S)~&\longrightarrow&~B&:&\{A,N_b\}_{k_{bs}}\\ \end{array}$$

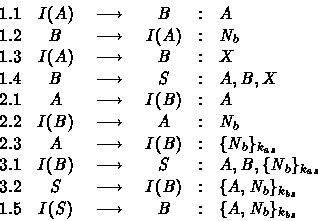
  In this scenario, the main session is session 1 where I is trying to convince B that he is the agent A . The intruder I sends the identity of A to the principal B which replies by sending a nonce $N_b$. As explained previously, at step 1.3, I can send any arbitrary value X because B is unable to perform any verification on the received message. At step 1.4, B sends (A, B, X) to S . At this step, one can imagine that S refuses the received message, but this is not important for the rest of the attack scenario. After this step I needs $\{N_b\}_{k_{as}}$ in order to progress in the protocol's steps. That explains why a parallel session with A is initiated.