We now define the model formally by describing how the overall global state and the individual principal local states are defined as well as by describing how actions update the state. The model consists of the asynchronous composition of a set of named, communicating processes, each augmented with a local store in which to keep track of the current information it ``knows'', and with a set of bindings for the variables appearing in the process. Each principal involved in the protocol is modelled as one of these processes and is described by a sequence of actions it is to perform and by the initial state of its local store. The initial state of the bindings is assumed to be empty. One process, the intruder, is not completely specified. Only the initial state of its local store is given and it is allowed to perform any ``realistic'' actions. For example, the intruder is not allowed to decrypt messages with a key it does not possess and it is not allowed to send messages that it cannot create with the information in its local store. But it is allowed to receive and send messages arbitrarily, possibly intercepting messages intended for other principals or possibly impersonating a trusted principal.
More formally, each principal is modelled as a 4-tuple ![]() , where:
, where:
The global state is then maintained as the composition of the
participating principals, along with the intruder process, a list of
permanent secrets, a list of temporary secrets, and a set of counters
indexed by the pairs of principals participating in protocol runs.
More formally, the global state is a 5-tuple ![]() , where:
, where:
The specific actions that a principal may perform can be divided into
internal actions and communication actions. The internal actions are
performed asynchronously. Any principal is allowed to perform an
internal action and interleaving is used to model all possible
behaviors when multiple principals can make a transition. We define a
transition relation ![]() between principals such that A
between principals such that A
![]() B if and only if principal A can take an
action and become a principal that behaves like B.
B if and only if principal A can take an
action and become a principal that behaves like B.
Communication actions consist of send and receive actions. Each receive action can potentially change the principal's local store, reflecting any new information it has ``learned.'' Communication actions can only occur in pairs and both principals make a transition simultaneously. These communication actions are also interleaved with the possible actions of other automata.
In order for a communication action to take place, the message being
sent must unify with the message being received. A message
s-msg from principal ![]() unifies with a message r-msg from principal
unifies with a message r-msg from principal ![]() , if there exist a
substitution
, if there exist a
substitution ![]() extending
extending ![]()
![]() , such that
, such that
![]() (s-msg) =
(s-msg) = ![]() (r-msg). If the
messages unify, then the following transitions can be taken:
(r-msg). If the
messages unify, then the following transitions can be taken:
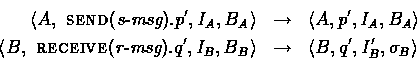
where ![]() .Because we require that s-msg unify with r-msg, if there
is already a pair (var, val) in B for some var
appearing in r-msg, then the corresponding value in s-msg
must be val. Thus the updates to B only add new bindings and
never change previous bindings.
.Because we require that s-msg unify with r-msg, if there
is already a pair (var, val) in B for some var
appearing in r-msg, then the corresponding value in s-msg
must be val. Thus the updates to B only add new bindings and
never change previous bindings.
For the most part internal actions are used to create or discover new information. For example, NEWNONCE is used to create a nonce. Nonces are globally distinct, and each NEWNONCE action creates a nonce that has not appeared up to that point in the protocol. The new nonce is added to the principal's local store. NEWSECRET works similarly, except that this is supposed to model generating a new session key which can then be used to encrypt messages. More formally:
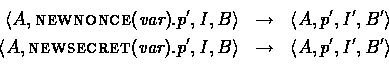
where in both cases, if val is the new value generated by the
action, then ![]() and
and ![]() . If the action was a NEWSECRET action, then
. If the action was a NEWSECRET action, then ![]() is updated in the global state as
well to
is updated in the global state as
well to ![]() .
.
Additionally, the intruder is allowed to perform a GETSECRET action which it can use to acquire a secret previously generated by a principal using NEWSECRET. This models the possibility of session keys being compromised. It allows us to have two classes of secrets, those which we assume to be ``permanent'' like a private key between a server and a trusted principal, and those secrets which are ``temporary'' such as session keys. We need to allow the intruder to obtain session keys in order to allow for the possibility of replay attacks which would allow the intruder to establish an old compromised key as a session key. However, we also need to restrict the the usage of GETSECRET or else the intruder would be allowed to compromise a session key immediately after it is generated and before it is ever used. For this reason, we only allow the intruder to perform a GETSECRET action to compromise a key which has already been established or used in a protocol. Formally,
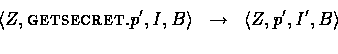
where for some val ![]() is updated to
is updated to ![]() {val}.
{val}.
Finally, we have four special actions BEGINIT, ENDINIT, BEGRESPOND, and ENDRESPOND. These are used to mark the beginning and the end of a principal's participation in a protocol. We use them to guarantee that if the principal named A finishes the protocol (performs ENDINIT(B)) then the principal named B has participated in the protocol (performed BEGRESPOND(A)). We do this by maintaining counters for each pair of principals participating in a protocol. More formally,
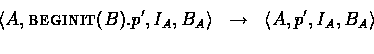
and we update the global state by setting the new value of ![]() :
: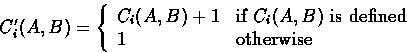
Similarly,
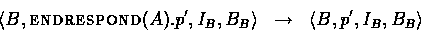
and we update the global state by setting the new value of ![]() :
: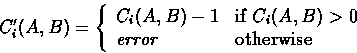
The definitions for BEGRESPOND and ENDINIT are identical
except that ![]() is updated in the global state instead of
is updated in the global state instead of ![]() .
.
The GETSECRET action may only be performed by the intruder,
while the rest of the actions may be performed by any principal. The
actions a particular honest principal may make are restricted to the
sequence of actions p that represent its role in the protocol. The
intruder has no such restriction and is allowed to make any action at
any time, provided that if it performs a SEND action with
message m , it must be the case that ![]() .
.
Recall that a trace is an alternating sequence of global states and actions and that we are interested in checking all possible traces. Clearly, there are a finite number of next states for each of the participants. In addition, while the intruder can generate an infinite number of messages, it is only allowed to send a finite number because each SEND much match with a RECEIVE. Since the there are a finite number of possible next states, we only consider a finite number of runs, we can perform a depth first search of the state space to generate all possible traces. We then check that no reachable state violates the security specification. Pseudocode for this algorithm can be found in figure 1.
Figure 1:
Model-checking algorithm
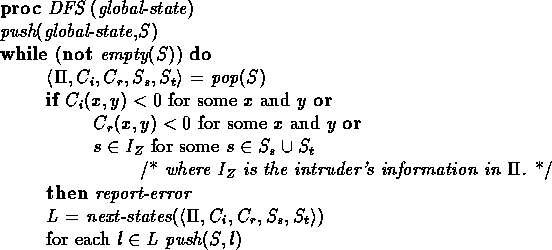
The remaining detail is how to maintain the local stores for the
principals. The local store is accessed in three places. First, if
principal ![]() sends a message m ,
then we must insure that
sends a message m ,
then we must insure that ![]() . Second, if the principal receives
message m , then we must update
. Second, if the principal receives
message m , then we must update ![]() to
to ![]() . Finally, we check every global state to see if
. Finally, we check every global state to see if ![]() for some
for some ![]() , where
, where ![]() is the
intruder's local store. It turns that these local stores are infinite
because of the closure operation. However, we never really need to
compute the entire closure; we need only determine if a particular
message is in the closure. So it suffices to represent the infinite
set with a finite set of ``generators.'' This is the topic of the
next section.
is the
intruder's local store. It turns that these local stores are infinite
because of the closure operation. However, we never really need to
compute the entire closure; we need only determine if a particular
message is in the closure. So it suffices to represent the infinite
set with a finite set of ``generators.'' This is the topic of the
next section.