Intuitively speaking, if B represents some set of information that
is known by a principal, then the principal also knows (can generate)
all the information in ![]() . In general
. In general ![]() is
an infinite set; however, we usually are not interested in the set of
everything that a principal knows, but instead whether or not a
specific message
is
an infinite set; however, we usually are not interested in the set of
everything that a principal knows, but instead whether or not a
specific message ![]() can be generated by a principal.
This leads us to the following definition.
can be generated by a principal.
This leads us to the following definition.
Let ![]() be a message. A derivation of x from
B is an alternating sequence of sets of messages and rule instances
written as follows:
be a message. A derivation of x from
B is an alternating sequence of sets of messages and rule instances
written as follows:
![]()
where:
For example, let ![]() . We derive
. We derive
![]() as follows:
as follows:
We would now like to introduce the notion of a normalized
derivation, but first we must introduce the notion of shrinking
rules and expanding rules by defining a metric ![]() . We then define a shrinking rule
to be a rule such that for every instance of the rule
. We then define a shrinking rule
to be a rule such that for every instance of the rule ![]() we have:
we have:
![]()
Analogously, an expanding rule is a rule for which every
instance ![]() we have:
we have:
![]()
We can now define a normalized derivation as follows:
![]()
is a normalized derivation if and only if for all ![]() is an expanding rule implies
is an expanding rule implies ![]() is an expanding rule for
all
is an expanding rule for
all ![]() . In other words, all shrinking rules appear to the
left of all expanding rules. Recall that in our notation,
. In other words, all shrinking rules appear to the
left of all expanding rules. Recall that in our notation, ![]() is
the rule instance
is
the rule instance ![]() ,
,
For example, in our model, we will define our metric ![]() inductively
as follows:
inductively
as follows:
Note that ![]() is well defined when
is well defined when ![]() , because the perfect encryption assumption implies
that
, because the perfect encryption assumption implies
that ![]() and
and ![]() . In the case
. In the case ![]() either
either ![]() is a substring of
is a substring of
![]() or
or ![]() is a substring of
is a substring of ![]() . Without loss of
generality, assume
. Without loss of
generality, assume ![]() . Then it must be the case
that
. Then it must be the case
that ![]() because we have
because we have ![]() . Therefore
. Therefore
![]()
The message derivation rules from section 5 can now be categorized. With these definitions, rules 3 and 5 are shrinking rules and rules 2 and 4 are expanding rules.
We now show that in our model, there is a derivation of x from B if and only if there is a normalized derivation of x from B . First we need the following lemma.
Lemma 1: Let ![]() be a derivation of length 2 such
that
be a derivation of length 2 such
that ![]() is an expanding rule and
is an expanding rule and ![]() is a shrinking rule.
Then there exists a derivation
is a shrinking rule.
Then there exists a derivation
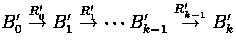 such that
such that
Proof:
Let ![]() and
and ![]()
In either case, ![]() , and the new derivation is
, and the new derivation is
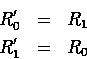
It is clear that ![]() .
.
If we also have ![]() and
and ![]() , then
, then ![]() . Therefore
. Therefore ![]() and we
let the new derivation consist only of
and we
let the new derivation consist only of
![]()
Otherwise, we must have that either ![]() is a substring of
is a substring of
![]() or
or ![]() is a substring of
is a substring of ![]() . Without loss of
generality, assume
. Without loss of
generality, assume ![]() . Then it must be the case
that
. Then it must be the case
that ![]() because we have
because we have ![]() . Then the new
derivation becomes:
. Then the new
derivation becomes:
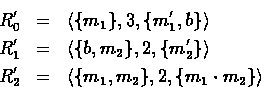
And we have that
![]()
Let ![]() and
and ![]()
One of our assumptions about encryption is that given m , the only
way to generate ![]() is by knowing m and k and using the
encryption algorithm. Therefore there are no
is by knowing m and k and using the
encryption algorithm. Therefore there are no ![]() and
and ![]() such
that
such
that ![]() . So, in this case,
. So, in this case, ![]() and the new derivation becomes
and the new derivation becomes
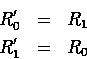
It is clear that ![]() .
.
Let ![]() and
and
![]()
Again, since we can't have ![]() , we must
have that
, we must
have that ![]() and the new derivation becomes
and the new derivation becomes
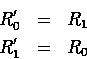
Again, ![]() .
.
Let ![]() and
and
![]()
In this case, we also have m' = m and k' = k , therefore ![]() and so the new derivation is:
and so the new derivation is:
![]()
Clearly, ![]() .
.
It must be the case that ![]() so the following is
a valid derivation:
so the following is
a valid derivation:
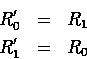
It is clear that ![]() .
.
Theorem 2: Let ![]() be a set of messages.
Then
be a set of messages.
Then ![]() if and only if x has a normalized
derivation from B .
if and only if x has a normalized
derivation from B .
Proof: If x has a normalized derivation from B then clearly
this is a derivation and by definition ![]() .
.
For the other direction, let ![]() . Then there exists
some derivation
. Then there exists
some derivation
![]()
such that ![]() . Let
. Let ![]() is a shrinking rule
and
is a shrinking rule
and ![]() such that
such that ![]() is an expanding rule }. If S
is empty, then
is an expanding rule }. If S
is empty, then ![]() is a normalized derivation and we are done.
Otherwise, we can induct on the size of S . Let
is a normalized derivation and we are done.
Otherwise, we can induct on the size of S . Let ![]() . By
repetitively using Lemma 1, we can move
. By
repetitively using Lemma 1, we can move ![]() to the left, until
either it is the leftmost rule, or it is immediately to the right of
another shrinking rule. Since the original derivation is finite and
since each time we apply Lemma 1, rule
to the left, until
either it is the leftmost rule, or it is immediately to the right of
another shrinking rule. Since the original derivation is finite and
since each time we apply Lemma 1, rule ![]() moves one slot to the
left, we need apply Lemma 1 only a finite number of times. If
moves one slot to the
left, we need apply Lemma 1 only a finite number of times. If ![]() becomes the leftmost rule, then clearly there are no expanding rules
to the left of
becomes the leftmost rule, then clearly there are no expanding rules
to the left of ![]() . If
. If ![]() is now immediately to the right of
another shrinking rule
is now immediately to the right of
another shrinking rule ![]() , then there are still no expanding
rules to the left of
, then there are still no expanding
rules to the left of ![]() because then there would be an expanding
rule to the left of
because then there would be an expanding
rule to the left of ![]() in the original derivation and so
in the original derivation and so ![]() and
and ![]() contradicting the minimality of r . Now we have a new
derivation of x ,
contradicting the minimality of r . Now we have a new
derivation of x , ![]() , which is still finite. Since the
application of Lemma 1 does not add any new shrinking rules, S' , the new
S , satisfies
, which is still finite. Since the
application of Lemma 1 does not add any new shrinking rules, S' , the new
S , satisfies ![]() . Furthermore |S'| = |S| - 1 , so by
the inductive hypothesis we can transform
. Furthermore |S'| = |S| - 1 , so by
the inductive hypothesis we can transform ![]() into a normalized
derivation of x .
into a normalized
derivation of x .
Corollary 3: Given ![]() and
and ![]() ,determining if
,determining if ![]() is decidable.
is decidable.
Proof: By Theorem 2, ![]() if and only if x has
a normalized derivation from B . We therefore try to find a
normalized derivation or show that none exists. First we repeatedly
apply shrinking rules to
if and only if x has
a normalized derivation from B . We therefore try to find a
normalized derivation or show that none exists. First we repeatedly
apply shrinking rules to ![]() creating new sets
creating new sets ![]() . Since
there are a finite number of rules, each rule creates a finite number
of new words, each smaller (by the metric
. Since
there are a finite number of rules, each rule creates a finite number
of new words, each smaller (by the metric ![]() ) than each of the
words used as an input to the rule, and
) than each of the
words used as an input to the rule, and ![]() is finite to begin,
there are only a finite number of
is finite to begin,
there are only a finite number of ![]() 's and hence we only apply
shrinking rules a finite number of times. Let us call this final set
's and hence we only apply
shrinking rules a finite number of times. Let us call this final set
![]() . Since
. Since ![]() is the result of repeatedly applying all
possible shrinking rules to B , x has a normalized derivation from
B if and only if it has a derivation from
is the result of repeatedly applying all
possible shrinking rules to B , x has a normalized derivation from
B if and only if it has a derivation from ![]() which uses only
expanding rules. Furthermore, the length of a minimal derivation of x
from
which uses only
expanding rules. Furthermore, the length of a minimal derivation of x
from ![]() is bounded by
is bounded by ![]() since each expanding rule creates
a words that are longer than the words used as inputs to the rule.
Since there are a finite number of expanding rules and
since each expanding rule creates
a words that are longer than the words used as inputs to the rule.
Since there are a finite number of expanding rules and ![]() is
itself finite, we can simply try all possible sequences of expanding
rules of length less than or equal to
is
itself finite, we can simply try all possible sequences of expanding
rules of length less than or equal to ![]() in a finite number of
steps. Therefore, this whole algorithm is guaranteed to terminate.
in a finite number of
steps. Therefore, this whole algorithm is guaranteed to terminate.
In the proof of Lemma 1, the majority of cases displayed a kind of
independence of rules. Intuitively, independence means that applying
one rule does not increase the set of things that can be derived using
the other rule. More formally, a shrinking rule s is
independent of an expanding rule e if for each pair of instances
![]() and
and ![]() we have one of the following:
we have one of the following:
Note that this property applied to almost all cases of Lemma 1 and that the only real work in proving Lemma 1 came from the case of the pairing rule and projection rule because these are not independent. The other pairs of rules were independent because of the ``perfect encryption assumption.'' In general, this exchanging property (Lemma 1) need only be shown for pairs of rules that are not independent.