On Tuza’s Conjecture in Dense Graphs

Rutgers graduate student Jake Baron and his advisor Jeff Kahn have provided a construction that shows that a bound on the size of minimum triangle edge cover of a graph G conjectured by Zsolt Tuza in 1981 is, in fact, asymptotically tight for an infinite family of dense graphs.

August 2016

missing Rutgers graduate student Jake Baron and his advisor Jeff Kahn have provided a construction [1] that shows that a bound on the size of minimum triangle edge cover of a graph G conjectured by Zsolt Tuza [2] in 1981 is, in fact, asymptotically tight for an infinite family of dense graphs. This disproves a more recent conjecture to the contrary by Raphael Yuster [3].

A triangle edge cover in the graph G is a set of edges of G such that every triangle of G contains an edge in the set. A minimum triangle edge cover in G is a triangle edge cover containing the fewest possible edges. Tuza’s conjecture relates the size of a minimum triagle edge cover in G to the size of a largest triangle packing, where a triangle packing is a set of triangles in G that are pairwise edge disjoint.

If we let C(G) denote the size of a minimum triangle edge cover and let P(G) denote the size of a maximum triangle packing in G, then it is relatively straightforward to see that P(G) ≤ C(G) ≤ 3P(G). The lower bound follows from the observation that at least one edge must be deleted from every triangle in the packing to obtain a triangle-free graph, while the upper bound follows because deleting every edge from every triangle in the packing would certainly eliminate all triangles from the graph.

Tuza’s conjecture is that C(G) ≤ 2P(G).

Tuza’s bound is tight for the complete graphs on four and five nodes. For the complete graph on four nodes, C = 2 and P = 1, while on five nodes C = 4 and P = 2. The latter is illustrated in the figure below.

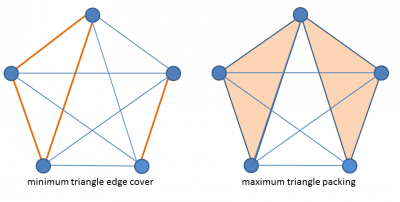K5-example.pngTuza’s bound remains tight for certain arbitrarily large graphs constructed by chaining together copies of the complete graph on four nodes in prescribed ways, but its status is open for more general large graphs. The best bound for general graphs (due to Penny Haxell [4]) assures that C(G) ≤ (66/23)P(G)—closer to the trivial bound than that conjectured by Tuza. On the other hand, results noted by Yuster [3] assure that Tuza’s bound holds asymptotically in graphs with quadratically large triangle covers. Specifically, if G is a graph containing n nodes for which C(G) ≥ b n2 for any fixed b > 0, then C(G) < (2+o(1)) P(G). Yuster then conjectured that the factor of 2 in Tuza’s conjecture is not, in fact, optimal in dense graphs in which the minimum triangle edge covers approach using half the edges in G (which is essentially as large as they could possibly be).

In light of Yuster’s conjecture, the question becomes whether the “2” in Tuza’s bound is tight for an infinite family of graphs containing quadratically-many triangles, or whether it could be improved (to say “3/2”) as the size of such a graph tends to infinity.

The construction that Baron and Kahn devised settles this question and disproves Yuster’s conjecture. It provides an infinite family of arbitrarily large dense graphs in which C(G) asymptotically approaches half the number of edges in G, and for which Tuza’s conjecture is asymptotically tight. The proof is rather involved, but their partly random construction ultimately guarantees, for any positive a, arbitrarily large graphs G of sufficient density that satisfy C(G) > (1-o(1)) |G|/2 and P(G) < (1+a)|G|/4.

These results are part of Baron’s PhD dissertation entitled “Two Problems on Cycles in Random Graphs” which he successfully defended on August 31, 2016. The results were also presented by Kahn at the DIMACS Workshop in Honor of Alan Hoffman. Baron received a 3-year fellowship associated with CCICADA, the homeland security center based at DIMACS, to support his graduate studies in mathematics. The fellowship was funded by a grant to DIMACS/CCICADA from the Department of Homeland Security.

A version of [1] is available on the arXiv: [arXiv paper]

Printable version of this story: [PDF]

References:
[1] J. D. Baron and J. Kahn, “Tuza’s Conjecture is Asymptotically Tight for Dense Graphs,” Combinatorics, Probability & Computing 25(5): 645-667 (2016).
[2] Z. Tuza, “Conjecture,” in A. Hajnal, L. Lovász, and V. T. Sós (eds.), Finite and Infinite Sets, Proc. Colloq. Math. Soc. Janos Bolyai, page 888. North-Holland, Amsterdam, 1981.
[3] R. Yuster, “Dense Graphs with a Large Triangle Cover Have a Large Triangle Packing,” Combinatorics, Probability & Computing, 21(6):952-962, (2012).
[4] P. Haxell, “Packing and Covering Triangles in Graphs,” Discrete Mathematics, 195:251-254, Jan 1999.