


Next: A Linear Approximation
Up: Network Design and Control
Previous: Network Control
For capacity planning, it is useful to consider the time required to
recover from a high-congestion event, as well as the likelihood of the
high-congestion event.
The likelihood of a high-congestion event in steady state can be
estimated using a large deviation principle (LDP) approximation.
The well-known Chernoff bound (e.g. see [7])
gives an upper bound to the stationary
tail probabilities of the aggregate level process, even for finitely many sources.
By Chebychev's
inequality, for all 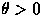 ,
,
| ![\begin{displaymath}
{\bf P}[L(t)\ge x]\le e^{-\theta x}{\bf E}[e^{\theta L(t)}]
...
...eta L_i(t)}]
=e^{-\theta x}\prod_i\sum_jp^i_j e^{\theta b^i_j},\end{displaymath}](img86.gif) |
(38) |
where bij is the required bandwidth and
pij is the steady-state probability of level j in source i,
as in (31).
Thus,
| ![\begin{displaymath}
{\bf P}[L(t)\ge x]\le e^{- I(x)},\quad{\rm where}\quad
I(x)=...
...eft(\theta x - \sum_i\log\sum_jp^i_j
e^{\theta b^i_j}\right)~.\end{displaymath}](img87.gif) |
(39) |
It can be shown [7] that such bounds are
asymptotically tight (have a large deviation limit) as the number of sources increases
provided the spectrum of behavior of individual sources is
sufficiently regular, yielding
the exponential approximation
| 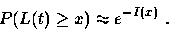 |
(40) |
Finding the rate function I will in general require
numerical solution of the variational expression (42). It can be shown
that the RHS of (42) is a concave function of 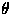 ,
and under mild
conditions it is differentiable also. Hence the supremum is achieved at the
unique
solution
,
and under mild
conditions it is differentiable also. Hence the supremum is achieved at the
unique
solution 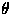 to the Euler-Lagrange equation
to the Euler-Lagrange equation
|  |
(41) |
Generally, it is not difficult to numerically determine
the supremum in (42) by location of the solution to
(44).
Example 6.1
In special cases the variational problem can be solved explicitly.
This is possible in the case of n homogeneous two-level sources.
Here we have bij=bj with 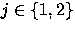 ,
, 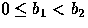 and p1+p2=1.
For this case,
and p1+p2=1.
For this case,
with y(x)=p1(x-b1)/(p2(b2-x))
for 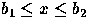 and
and 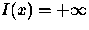 elsewhere.
elsewhere.
We now show how to estimate the time to recover from the high-congestion
event,
where the high-congestion event is a large initial bandwidth x.
We understand recovery to occur when the aggregate bandwidth is again
less than or equal to the capacity c.
In applications, we suggest examining the function of
aggregate bandwidth giving both
the
probability of reaching that level and the recovery time from that level to assess whether or not capacity
is adequate to meet demand.
We assume that recovery occurs when the
aggregate bandwidth drops below a level c, where x > c > m,
with x being the initial level and m being the steady-state mean.
Given that we know the current level of each level process, we know that the
remaining holding time (and also the age) is
distributed according to the level-holding-time stationary-excess distribution in (32).
We use the LDP to approximate the conditional distribution of the
level process for each source (in steady state).
The idea is to perform the appropriate change of measure (tilting)
corresponding to the rare event.
Given that 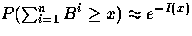 for I(x) in (42), the LDP
approximation is
for I(x) in (42), the LDP
approximation is
|  |
(42) |
where 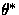 yields the supremum in (42).
Put another way, comparing (47) with (44) we see
that
yields the supremum in (42).
Put another way, comparing (47) with (44) we see
that 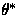 is chosen to make the expectation of
is chosen to make the expectation of 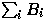 equal
to x under the distribution
equal
to x under the distribution  .In the homogeneous
case, equality in (47) in the limit as the number of sources increases is due to
the conditional limit theorem of Van Campenhout and Cover [21].
The limit can be extended to cover suitably regular
heterogeneity in the bij, e.g., finitely many types of source.
.In the homogeneous
case, equality in (47) in the limit as the number of sources increases is due to
the conditional limit theorem of Van Campenhout and Cover [21].
The limit can be extended to cover suitably regular
heterogeneity in the bij, e.g., finitely many types of source.
We thus approximate the conditional bandwidth process by
for 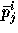 in (4.3)
which has Laplace transform
in (4.3)
which has Laplace transform
|  |
(43) |
The Laplace transform 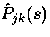 in (49) was derived in
Theorem 4.1. We can numerically invert it to calculate the
conditional mean as a function of time.
We then can
determine when
E(B(t)|B(0) = x) first falls below c.
In general, this conditional mean need not be a
decreasing function, so that care is needed in the definition,
but we expect it to be decreasing for suitably small t
because the initial point B(0) is unusually high.
in (49) was derived in
Theorem 4.1. We can numerically invert it to calculate the
conditional mean as a function of time.
We then can
determine when
E(B(t)|B(0) = x) first falls below c.
In general, this conditional mean need not be a
decreasing function, so that care is needed in the definition,
but we expect it to be decreasing for suitably small t
because the initial point B(0) is unusually high.



Next: A Linear Approximation
Up: Network Design and Control
Previous: Network Control
Nick Duffield
11/24/1997
![\begin{displaymath}
{\bf P}[L(t)\ge x]\le e^{- I(x)},\quad{\rm where}\quad
I(x)=...
...eft(\theta x - \sum_i\log\sum_jp^i_j
e^{\theta b^i_j}\right)~.\end{displaymath}](img87.gif)
![]() ,
and under mild
conditions it is differentiable also. Hence the supremum is achieved at the
unique
solution
,
and under mild
conditions it is differentiable also. Hence the supremum is achieved at the
unique
solution ![]() to the Euler-Lagrange equation
to the Euler-Lagrange equation

![]() for I(x) in (42), the LDP
approximation is
for I(x) in (42), the LDP
approximation is

