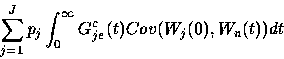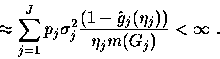Next: Conclusions
Up: Network Design and Control
Previous: A Linear Approximation
Useful characterizations of the aggregate and single-source bandwidth
processes are their
(auto)covariance
functions.
The covariance function may help in evaluating the fitting.
We now show that we can effectively compute
the covariance function
for our traffic source model.
Let 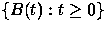 and
and 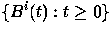 be stationary versions of the
aggregate and source-i bandwidth processes, respectively.
Assuming that the single-source bandwidth processes are mutually
independent, the covariance function of the aggregate bandwidth
process is the sum of the single-source covariance functions, i.e.,
be stationary versions of the
aggregate and source-i bandwidth processes, respectively.
Assuming that the single-source bandwidth processes are mutually
independent, the covariance function of the aggregate bandwidth
process is the sum of the single-source covariance functions, i.e.,
|  |
(47) |
Hence, it suffices to focus on a single source, and we do, henceforth
dropping the superscript i.
In general,
where the steady-state mean m is as in
(30) and (31) and
where gje(x) = Gcj(x)/m(Gj) is the density of Gje, and
the second term captures the effect of the within-level variation process.
In (56) bj is the bandwidth in level j, pj is the
steady-state probability of level j, gje(x) = Gcj(x)/m(Gj)
with Gj the level-j holding-time cdf and m(Gj) its mean, and
Pjk(t|x) is the transition probability, whose matrix of Laplace
transforms is given in Theorem 3.1 of [10]. We can thus calculate S(t)
by numerically inverting its Laplace transform
To treat the second term in (58),
we can assume an approximate functional form for the
covariance of the within-level variation process W(t).
For example, if
| 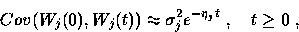 |
(49) |
then
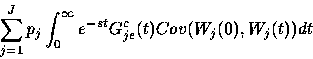
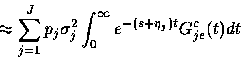
| 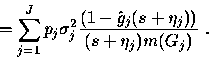 |
(50) |
Thus, with approximation (59), we have a closed-form
expression for the second term of the
transform  in (58).
For each required s in
in (58).
For each required s in  , we need to perform one
numerical integration in the first term of (58), after calculating the integrand as a function
of x.
, we need to perform one
numerical integration in the first term of (58), after calculating the integrand as a function
of x.
A major role is played by the asymptotic variance 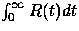 .For example, the heavy-traffic approximation for the workload process in a queue
with arrival process
.For example, the heavy-traffic approximation for the workload process in a queue
with arrival process 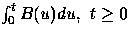 ,depends on the process
,depends on the process 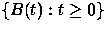 only
through its rate EB(0) and
its asymptotic variance; see
Iglehart and Whitt [17].
The input process is said to exhibit long-range
dependence when this integral is infinite.
The source traffic model shows that long-range dependence stems from level holding-time
distributions with infinite variance.
only
through its rate EB(0) and
its asymptotic variance; see
Iglehart and Whitt [17].
The input process is said to exhibit long-range
dependence when this integral is infinite.
The source traffic model shows that long-range dependence stems from level holding-time
distributions with infinite variance.
Theorem 7132
If a level holding-time cdf Gj has infinite variance, then the
source bandwidth process exhibits long-range dependence, i.e.,
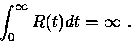
Proof.
In (57) we have the component
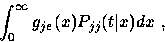
which in turn has the
component
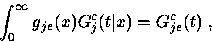
but
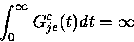
if Gj has infinite variance.
(As can be seen using integration by parts,
the integral is the mean of Gje;
see p. 150 of Feller [13].
In general, Gje has 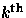 moment
mk+1 (Gj )/(k+1)m1 (Gj ),
where mk (Gj ) is the
moment
mk+1 (Gj )/(k+1)m1 (Gj ),
where mk (Gj ) is the 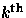 moment of Gj.)
moment of Gj.)
Note that if approximation (59) holds, then the level
process contributes to long-range dependence, but the within-level
variation process does not,
because
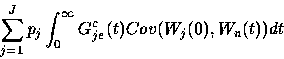
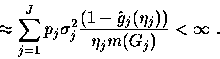



Next: Conclusions
Up: Network Design and Control
Previous: A Linear Approximation
Nick Duffield
11/24/1997
![]() and
and ![]() be stationary versions of the
aggregate and source-i bandwidth processes, respectively.
Assuming that the single-source bandwidth processes are mutually
independent, the covariance function of the aggregate bandwidth
process is the sum of the single-source covariance functions, i.e.,
be stationary versions of the
aggregate and source-i bandwidth processes, respectively.
Assuming that the single-source bandwidth processes are mutually
independent, the covariance function of the aggregate bandwidth
process is the sum of the single-source covariance functions, i.e.,

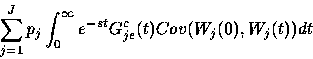
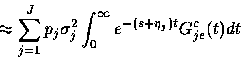
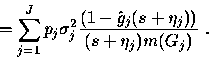
![]() .For example, the heavy-traffic approximation for the workload process in a queue
with arrival process
.For example, the heavy-traffic approximation for the workload process in a queue
with arrival process ![]() ,depends on the process
,depends on the process ![]() only
through its rate EB(0) and
its asymptotic variance; see
Iglehart and Whitt [17].
The input process is said to exhibit long-range
dependence when this integral is infinite.
The source traffic model shows that long-range dependence stems from level holding-time
distributions with infinite variance.
only
through its rate EB(0) and
its asymptotic variance; see
Iglehart and Whitt [17].
The input process is said to exhibit long-range
dependence when this integral is infinite.
The source traffic model shows that long-range dependence stems from level holding-time
distributions with infinite variance.![]()
![]()
![]()
![]()